فهرست مطالب  (کلیک کنید تا مرور گر به آن نقطه از صفحه برود):

نمونه گیری چیست؟

خطای نمونه گیری

1- روش های نمونه گیری احتمالاتی

۱-۱- نمونه گیری تصادفی ساده

۲-۱- نمونه گیری طبقه ای

۳-۱- نمونه گیری خوشه ای

۴-۱- نمونه گیری چند مرحله ای

۵-۱- نمونه گیری سیستماتیک

۲- تعیین حجم نمونه

۱-۲- تعیین اندازه نمونه بر اساس جدول های آماده

۲-۲- تعیین حجم نمونه بر اساس نظر پژوهش گر

۳-۲- تعیین اندازه نمونه بر اساس محاسبات آماری

تعیین اندازه نمونه با فرمول کوکران

{برو به فهرست}

نمونه گیری چیست؟

نمونه گیری یعنی اینکه بخش کوچکی از جامعه آماری را بررسی نموده و نتایج آنرا به کل جامعه تعمیم دهیم. ضرب المثل رایج در میان مردم که به نمونه گیری اشاره دارد این است: “مشت نمونه خروار است”.  {برو به فهرست}

زیرا به عنوان مثال یک مشتی که شما به تصادف از میان یک خروار گندم بر می دارید، نماینده آن خروار گندم است (از نظر کیفیت یا اندازه یا مشخصه ای دیگر).

خطای نمونه گیری

نتایج یک بررسی نمونه ای هیچ گاه با قطعیت و حقیقت همراه نیست. زیرا نتایج تحت تاثیر خطایی تحت عنوان خطای نمونه گیری قرار دارد که ناشی از انتخاب بخشی از جامعه به جای کل جامعه است.

میزان خطای نمونه گیری را می توان با افزایش اندازه ی نمونه کاهش داد. اما از طرف دیگر، زیاد کردن اندازه نمونه روی عامل های متعددی از جمله حجم عملیات میدانی و هزینه ی آمار گیری تاثیر نامطلوب دارد.    {برو به فهرست}

در این مبحث ابتدا به بیان انواع روش های نمونه گیری و سپس روشهای تعیین حجم نمونه در پایان نامه ها و مقالات می پردازیم.

1- روش های نمونه گیری احتمالاتی

روشهاي نمونه گيري آماري كه عموما در تحقيقات و پژوهشهاي كاربردي مورد استفاده قرار مي گيرد، در این مقاله معرفی شده است. قابل ذکر است تمام روشهای معرفی شده زیر از نوع روش های نمونه گیری احتمالاتی می باشند. روش نمونه گیری احتمالاتی، فرآیندی است که احتمال انتخاب هر کدام از واحدهای جامعه از قبل مشخص و معلوم و غیر صفر است. در این روش هر واحد نمونه با احتمالی مشخص از جامعه استخراج می شود.     {برو به فهرست}

قابل ذکر چنانچه مایلید در خصوص نمونه گیری غیر احتمالاتی نیز اطلاعاتی بدست آورید، صفحه نمونه گیری غیر احتمالی را مشاهده و مطالعه نمایید.

1-1- نمونه گيري تصادفي ساده

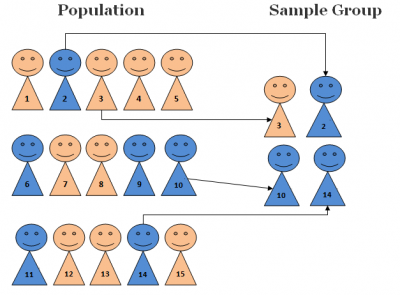
روش نمونه گیری تصادفی ساده، ساده ترین روش نمونه گیری احتمالاتی است.

در اين نوع نمونه گيري به هر يك از افراد جامعه احتمال مساوي داده مي‌شود تا در نمونه انتخاب شوند. به عبارت ديگر اگر حجم افراد جامعه N  و حجم نمونه را n   فرض كنيم، احتمال انتخاب هر فرد جامعه در نمونه مساوي n/N  است.  انتخاب نمونه تصادفي ساده را به سه شيوه مي‌توان انجام داد: شيوه اول به صورت قرعه كشي، شيوه دوم با استفاده از جدول اعداد تصادفي و شیوه سوم با نرم افزارهای رایانه ای.

براي انتخاب يك نمونه تصادفي ساده به شيوه قرعه كشي بايد با توجه به چارچوب نمونه گيري از ميان افراد جامعه يك نمونه به حجم نمونه مورد نظر از ميان افراد فهرست شده به حكم قرعه انتخاب كرد.

در شيوه دوم، بايد حجم جامعه مورد نظر را N   قرار داد. سپس به تعداد ارقام تشكيل دهنده حجم جامعه ، ستون يك رقمي در جدول اعداد تصادفي منظور داشت (مثلا حجم جامعه 50 شامل دو رقم است بنابراين دو ستون يك رقمي در جدول اختيار مي كنيم). پس از آن يك نقطه شروع به طور تصادفي براي انتخاب واحدها اختيار كرد. سرانجام عمل انتخاب را از اين نقطه آغاز كرده و هر عددي كه كوچكتر يا مساوي N باشد را به عنوان نمونه انتخابي منظور داشت. در شیوه سوم نیز از نرم افزارهای رایانه ای برای انتخاب نمونه تصادفی استفاده می شود.     {برو به فهرست}

قابل ذکر است که برای انتخاب یک نمونه به روش تصادفی ساده، از دو شیوه با جای گذاری و بدون جایگزاری استفاده می شود. که در روش نمونه گیری با جای گذاری، هر واحد نمونه بعد از انتخاب، دو مرتبه به جامعه بازگردانده می شود و این احتمال وجود دارد که در انتخاب های بعدی، آن واحد مجددا در نمونه انتخاب شود.

2-1- نمونه گيري طبقه اي

نمونه گيري طبقه اي (نمونه گیری تصادفی با طبقه بندی) هنگامی مناسب است که بتوانیم جامعه آماری را نسبت به صفت مربوطه طوری تقسیم کنیم که واحدها در داخل طبقات از نظر صفت مربوطه شبیه به هم باشند.

در این نوع نمونه گیری، واحدهاي جامعه مورد مطالعه در طبقه هايي كه از نظر صفت متغير همگن تر هستند، گروه بندي مي شوند، تا تغييرات آنها در درون گروه ها كمتر شود. پس از آن از هر يك از طبقه ها، تعدادي نمونه به صورت تصادفي انتخاب مي‌شود. معمولا براي طبقه بندي واحدهاي جامعه، متغيري به عنوان ملاك در نظر گرفته مي‌شود كه با صفت متغير مورد مطالعه بستگي داشته باشد.

براي مثال به منظور بررسي نسبت قبول شدگان در پايه پنجم آموزش ابتدايي در شهر تهران و رابطه آن با محل جغرافيايي دبستان، مي‌توان ابتدا دبستان هاي شهر تهران را بر حسب محل دبستان به پنج طبقه تقسيم كرد: طبقه يك شامل دبستان هاي شمال غربي، طبقه دوم دبستان هاي شمال شرقي، طبقه سوم دبستان هاي مركزي شهر، طبقه چهارم دبستان هاي جنوب غربي و طبقه پنجم دبستان هاي جنوب شرقي. پس از آن از هر طبقه تعدادي دبستان به روش تصادفي ساده انتخاب كرد.     {برو به فهرست}

در نمونه گيري طبقه اي حجم نمونه (n) را به شيوه هاي مختلف مي‌توان ميان طبقه ها تقسيم كرد. ساده ترين شيوه، تقسيم مساوي تعداد نمونه ميان طبقه هاست. ساير شيوه ها شامل انتساب بهينه و انتساب متناسب است. در انتساب متناسب به تناسب حجم هر طبقه، حجم نمونه در آن طبقه تعيين مي‌گردد.

3-1- نمونه گيري خوشه اي

در صورتي كه فهرست كامل افراد جامعه مورد مطالعه در دسترس نباشد مي‌توان افراد جامعه را در دسته هايي خوشه بندي كرد. سپس از ميان خوشه ها به تصادف نمونه گيري به عمل آورده و تمام حجم خوشه را سرشماري مي كنيم. براي اين منظور فهرستي از اين خوشه ها تهيه مي‌شود و از آن به عنوان چارچوب نمونه گيري استفاده مي‌شود.

به طور کلی نمونه گیری تصادفی خوشه ای به دو دلیل عمده زیر به کار می رود:

الف- صرفه جویی در وقت و هزینه

ب- موجود نبودن چارچوب نمونه گیری.

نمونه گيري خوشه اي در صورتي كارآمدتر از نمونه گيري تصادفي ساده است كه چارچوب نمونه گيري (فهرست كامل افراد جامعه) در دسترس نباشد. در واقع وقتی هزینه ساخت چارچوب نمونه گیری از واحد ها (فهرست واحدها) زیاد باشد یا چارچوبی از آن ها در دست نباشد، نمونه گیری خوشه ای به کار می رود.

بايد توجه داشت كه هر چه حجم خوشه ها افزايش يابد و تشابه افراد آن از نظر صفت متغير مورد بررسي بيشتر باشد، دقت نمونه گيري خوشه اي كمتر مي‌شود.

• تفاوت بین نمونه گیری خوشه ای با نمونه گیری طبقه ای

  

همانطور که تصویر فوق نیز گویاست، تفاوت های بارز زیر را بین نمونه گیری های تصادفی خوشه ای و طبقه ای همواره باید مد نظر داشت:

الف-در نمونه گیری تصادفی طبقه ای از هر طبقه تعدادی را به عنوان نمونه انتخاب می کنیم در صورتی که در نمونه گیری تصادفی خوشه ای، نمونه از تعدادی از خوشه ها انتخاب می شود.          {برو به فهرست}

ب- دقت نمونه گیری تصادفی طبقه ای در ارتباط مستقیم با همگنی درون طبقات و نا همگنی بین طبقات است. اما دقت نمونه گیری تصادفی خوشه ای در ارتباط مستقیم با ناهمگنی درون خوشه ها و همگنی بین خوشه هاست.

4-1- نمونه گیری چند مرحله ای

در نمونه گیری چند مرحله ای، افراد جامعه با توجه به سلسله مراتب (از واحدهای بزرگ تر به کوچک تر) از انواع واحدهای جامعه انتخاب می شوند. یک مثال می تواند این نوع نمونه گیری را روشن کند:

برای مثال در برآورد توانایی ریاضی دانش آموزان پایه پنجم ابتدایی در یک منطقه آموزش و پرورش، می توان دانش آموزان را در سه مرحله با استفاده از واحدهای نمونه گیری مختلف زیر به صورت زیر انتخاب کرد:

واحد مرحله اول:          دبستان           دبستان 1              دبستان 2       ……           دبستان 10

واحد مرحله دوم:         کلاس           کلاس 1 و 2            کلاس 3 و 4    …..           کلاس 19 و 20

واحد مرحله سوم:  دانش آموزش 1، 2، 3، . . . . 58، 59، 60

در مثال فوق ابتدا جامعه دانش آموزان ابتدایی پایه پنجم, به دبستان هایی تقسیم شده است. در این مرحله که مرحله اول نمونه گیری است، از میان دبستان های انتخاب شده دو کلاس (واحد مرحله دوم) انتخاب شده است. در اینجا از دبستان شماره یک، کلاس های 1 و 2 پایه پنجم و از دبستان شماره دوم کلاس های 3 و 4 پایه پنجم و بالاخره از دبستان دهم کلاس های 19 و 20 پایه پنجم به طور تصادفی انتخاب شده اند.

در مجموع 60 دانش آموز (3*2*10 = 60) از 20 کلاس و 10 دبستان انتخاب شده است.     {برو به فهرست}

نمونه گیری چند مرحله ای در مقایسه با نمونه گیری خوشه ای از دقت بیشتری برخوردار است. زیرا در نمونه گیری چند مرحله ای واحدهای نمونه مرحله نهایی در سطح جامعه پراکنده شده و تغییرات متغیر مورد بررسی در نمونه، معرف تغییرات مورد مطالعه در جامعه است. در حالی که در نمونه گیری خوشه ای چنین امری میسر نمی باشد.

5-1- نمونه گیری سیستماتیک

روش نمونه گیری تصادفی سیستماتیک، به روش انتخاب تصادفی دنباله ای از واحدهای جامعه که به یک اندازه ثابت از هم فاصله دارند، دلالت دارد. به عبارت دیگر، در این روش اگر k فاصله نمونه گیری باشد، ابتدا یک عدد تصادفی از بین اعداد 1 تا k، به عنوان نقطه شروع انتخاب شده و سپس با افزودن ضریب های صحیح k به این نقطه شروع، سایر واحدهای نمونه ای مشخص می شوند.

تصویر زیر نمونه گیری سیستماتیک را بیان می کند که در آن فاصله نمونه گیری 3 است:

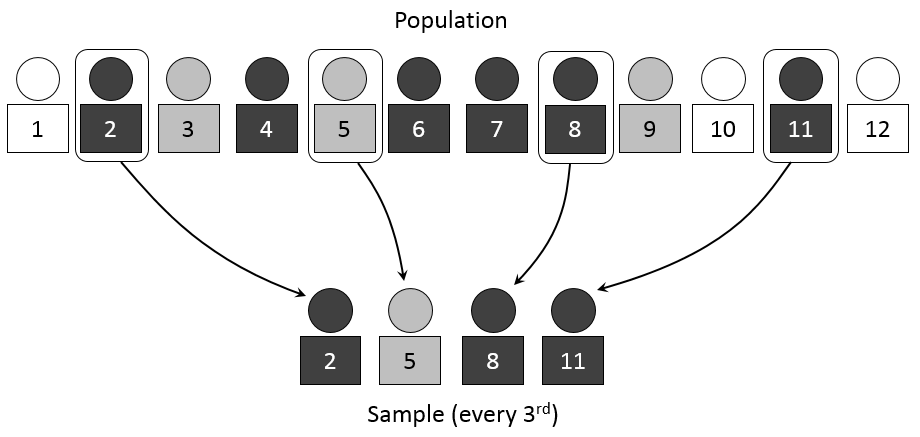
دقت نمونه گیری تصادفی سیستماتیک وقتی واحدهای جامعه به طور تصادفی مرتب شده باشند، مساوی با نمونه گیری تصادفی ساده و زمانی که واحدهای جامعه بر اساس صفتی مرتبط با صفت مورد برآورد مرتب شده باشند، بهتر از نمونه گیری تصادفی ساده و حتی بهتر از نمونه گیری طبقه ای است. به علاوه اجرای آن ساده و به کارگیری آن کم هزینه است.

توجه شود که این روش نمونه گیری را حتی در مواردی که از اندازه جامعه مطلع نیستیم می توان با انتخاب مناسب فاصله نمونه گیری(k) با توجه به ساختار جامعه به کار گرفت.

• مثال نمونه گیری سیستماتیک

به طور مثال برای انتخاب یک نمونه تصادفی به اندازه n از افرادی که به یک بانک مراجعه می کنند می توان از این شیوه نمونه گیری استفاده کرد.          {برو به فهرست}

به این ترتیب که از هر k نفر، یک نفر را به عنوان نمونه انتخاب کرده و این کار را تا جایی ادامه دهیم که تمام n واحد نمونه گیری انتخاب شوند.

2- تعيين حجم نمونه

اخذ تصميم درباره حجم نمونه, از لحاظ تامين ميزان دقت نتايج نمونه گيری و صرفه جويي در مقدار وقت و هزينه, از اهميتی خاص برخوردار است. بديهی است که بزرگ بودن حجم نمونه موجب صرف هزينه و وقت زياد, و کوچک بودن حجم نمونه موجب عدم دقت کافی برآوردها می شود.            {برو به فهرست}

برای تعیین اندازه نمونه، چند راه پیش رو داریم که در ادامه هر کدام را شرح می دهیم:

1-2- تعیین اندازه نمونه بر اساس جدول های آماده

یکی از راه های تعیین اندازه نمونه استفاده از جدول هایی است که برای همین منظور تهیه شده است. در این جدول ها با توجه به اندازه جامعه (N)، اندازه نمونه (n) تعیین شده است. براي محاسبه حجم نمونه با این روش و مشاهده جدول نمونه گیری مورگان این صفحه را ببینید: محاسبه آنلاین حجم نمونه با روش جدول مورگان

2-2- تعیین حجم نمونه بر اساس نظر پژوهش گر

در این روش پژوهش گر و دانشجو با در نظر گرفتن عامل هایی مثل بودجه، زمان، نیروی انسانی ماهر، امکانات و امثال آن درصدی از جامعه را به عنوان نمونه انتخاب می کند. برخی از پژوهشگران حداقل اندازه نمونه را 10 درصد اندازه جامعه ذکر کرده اند.

3-2- تعیین اندازه نمونه بر اساس محاسبات آماری

متداول ترین روش محاسبه اندازه نمونه، استفاده از محاسبات آماری است. در این روش پژوهش گر ابتدا توسط یک آزمون مقدماتی، پارامترهای مورد نیاز جامعه آماری را مشخص کرده و سپس با استفاده از فرمول های مربوط، اندازه نمونه را محاسبه می کند. عامل های موثر بر تعداد نمونه عبارتند از:

1- سطح معنی داری،

2-میزان دقت برآورد مورد نظر و یا میزان خطای حاشیه ای،

3- تغییر پذیری متغیر مورد نظر (واریانس یا پراکنش)،

4- روش نمونه گیری،

5- اندازه جامعه آماری،                      {برو به فهرست}

6- هزینه و امکانات اجرایی.

• تعیین اندازه نمونه با فرمول کوکران

براي اينکه بتوانيد بر اساس محاسبات آماری و به صورت آنلاين حجم نمونه پايان نامه خويش را محاسبه نماييد بر روي لينک زیر کليک نماييد. در این صفحه به صورت آنلاین و همراه با فیلم آموزشی رایگان، محاسبه حجم نمونه با روش کوکران در دو حالت ارائه می گردد:

محاسبه آنلاين حجم نمونه با فرمول کوکران

https://www.spss-iran.com/